AES, like all good block ciphers, performs a "keyed permutation". This means that it maps every possible input block to a unique output block, with a key determining which permutation to perform.

A "block" just refers to a fixed number of bits or bytes, which may represent any kind of data. AES processes a block and outputs another block. We'll be specifically talking the variant of AES which works on 128 bit (16 byte) blocks and a 128 bit key, known as AES-128.

Using the same key, the permutation can be performed in reverse, mapping the output block back to the original input block. It is important that there is a one-to-one correspondence between input and output blocks, otherwise we wouldn't be able to rely on the ciphertext to decrypt back to the same plaintext we started with.

What is the mathematical term for a one-to-one correspondence?

If a block cipher is secure, there should be no way for an attacker to distinguish the output of AES from a random permutation of bits. Furthermore, there should be no better way to undo the permutation than simply bruteforcing every possible key. That's why academics consider a cipher theoretically "broken" if they can find an attack that takes fewer steps to perform than bruteforcing the key, even if that attack is practically infeasible.

How difficult is it to bruteforce a 128-bit keyspace? Somebody estimated that if you turned the power of the entire Bitcoin mining network against an AES-128 key, it would take over a hundred times the age of the universe to crack the key.

It turns out that there is an attack on AES that's better than bruteforce, but only slightly – it lowers the security level of AES-128 down to 126.1 bits, and hasn't been improved on for over 8 years. Given the large "security margin" provided by 128 bits, and the lack of improvements despite extensive study, it's not considered a credible risk to the security of AES. But yes, in a very narrow sense, it "breaks" AES.

Finally, while quantum computers have the potential to completely break popular public-key cryptosystems like RSA via Shor's algorithm, they are thought to only cut in half the security level of symmetric cryptosystems via Grover's algorithm. This is one reason why people recommend using AES-256, despite it being less performant, as it would still provide a very adequate 128 bits of security in a quantum future.

What is the name for the best single-key attack against AES?

To achieve a keyed permutation that is infeasible to invert without the key, AES applies a large number of ad-hoc mixing operations on the input. This is in stark contrast to public-key cryptosystems like RSA, which are based on elegant individual mathematical problems. AES is much less elegant, but it's very fast.

At a high level, AES-128 begins with a "key schedule" and then runs 10 rounds over a state. The starting state is just the plaintext block that we want to encrypt, represented as a 4x4 matrix of bytes. Over the course of the 10 rounds, the state is repeatedly modified by a number of invertible transformations.

Each transformation step has a defined purpose based on theoretical properties of secure ciphers established by Claude Shannon in the 1940s. We'll look closer at each of these in the following challenges.

Here's an overview of the phases of AES encryption: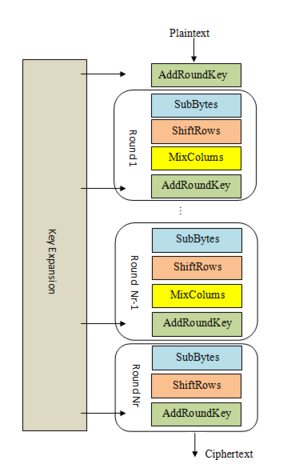



1. KeyExpansion or Key Schedule

 From the 128 bit key, 11 separate 128 bit "round keys" are derived: one to be used in each AddRoundKey step.

2. Initial key addition

 AddRoundKey - the bytes of the first round key are XOR'd with the bytes of the state.

3. Round - this phase is looped 10 times, for 9 main rounds plus one "final round"

 a) SubBytes - each byte of the state is substituted for a different byte according to a lookup table ("S-box").

 b) ShiftRows - the last three rows of the state matrix are transposed—shifted over a column or two or three.

 c) MixColumns - matrix multiplication is performed on the columns of the state, combining the four bytes in each column. This is skipped in the final round.

 d) AddRoundKey - the bytes of the current round key are XOR'd with the bytes of the state.

Included is a bytes2matrix function for converting our initial plaintext block into a state matrix. Write a matrix2bytes function to turn that matrix back into bytes, and submit the resulting plaintext as the flag.

Challenge files:
  - matrix.py

Resources:
  - YouTube: AES Rijndael Cipher explained as a Flash animation

We're going to skip over the finer details of the KeyExpansion phase for now. The main point is that it takes in our 16 byte key and produces 11 4x4 matrices called "round keys" derived from our initial key. These round keys allow AES to get extra mileage out of the single key that we provided.

The initial key addition phase, which is next, has a single AddRoundKey step. The AddRoundKey step is straightforward: it XORs the current state with the current round key.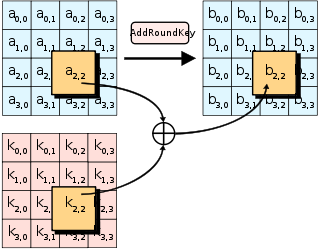



AddRoundKey also occurs as the final step of each round. AddRoundKey is what makes AES a "keyed permutation" rather than just a permutation. It's the only part of AES where the key is mixed into the state, but is crucial for determining the permutation that occurs.

As you've seen in previous challenges, XOR is an easily invertible operation if you know the key, but tough to undo if you don't. Now imagine trying to recover plaintext which has been XOR'd with 11 different keys, and heavily jumbled between each XOR operation with a series of substitution and transposition ciphers. That's kinda what AES does! And we'll see just how effective the jumbling is in the next few challenges.

Complete the add_round_key function, then use the matrix2bytes function to get your next flag.

Challenge files:
  - add_round_key.py

The first step of each AES round is SubBytes. This involves taking each byte of the state matrix and substituting it for a different byte in a preset 16x16 lookup table. The lookup table is called a "Substitution box" or "S-box" for short, and can be perplexing at first sight. Let's break it down.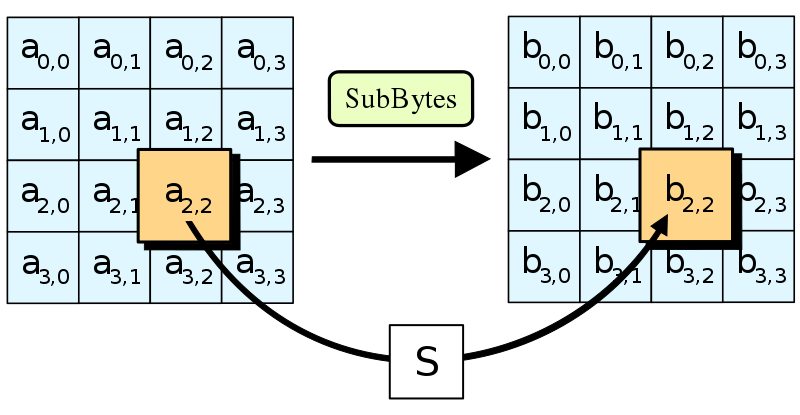



In 1945 American mathematician Claude Shannon published a groundbreaking paper on Information Theory. It identified "confusion" as an essential property of a secure cipher. "Confusion" means that the relationship between the ciphertext and the key should be as complex as possible. Given just a ciphertext, there should be no way to learn anything about the key.

If a cipher has poor confusion, it is possible to express a relationship between ciphertext, key, and plaintext as a linear function. For instance, in a Caesar cipher, ciphertext = plaintext + key. That's an obvious relation, which is easy to reverse. More complicated linear transformations can be solved using techniques like Gaussian elimination. Even low-degree polynomials, e.g. an equation like x^4 + 51x^3 + x, can be solved efficiently using algebraic methods. However, the higher the degree of a polynomial, generally the harder it becomes to solve – it can only be approximated by a larger and larger amount of linear functions.

The main purpose of the S-box is to transform the input in a way that is resistant to being approximated by linear functions. S-boxes are aiming for high non-linearity, and while AES's one is not perfect, it's pretty close. The fast lookup in an S-box is a shortcut for performing a very nonlinear function on the input bytes. This function involves taking the modular inverse in the Galois field 2**8 and then applying an affine transformation which has been tweaked for maximum confusion. The simplest way to express the function is through the following high-degree polynomial: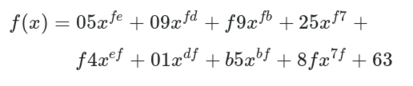



To make the S-box, the function has been calculated on all input values from 0x00 to 0xff and the outputs put in the lookup table.

Implement sub_bytes, send the state matrix through the inverse S-box and then convert it to bytes to get the flag.

Challenge files:
  - sbox.py

We've seen how S-box substitution provides confusion. The other crucial property described by Shannon is "diffusion". This relates to how every part of a cipher's input should spread to every part of the output.

Substitution on its own creates non-linearity, however it doesn't distribute it over the entire state. Without diffusion, the same byte in the same position would get the same transformations applied to it each round. This would allow cryptanalysts to attack each byte position in the state matrix separately. We need to alternate substitutions by scrambling the state (in an invertible way) so that substitutions applied on one byte influence all other bytes in the state. Each input into the next S-box then becomes a function of multiple bytes, meaning that with every round the algebraic complexity of the system increases enormously.

An ideal amount of diffusion causes a change of one bit in the plaintext to lead to a change in statistically half the bits of the ciphertext. This desirable outcome is called the Avalanche effect.

The ShiftRows and MixColumns steps combine to achieve this. They work together to ensure every byte affects every other byte in the state within just two rounds.

ShiftRows is the most simple transformation in AES. It keeps the first row of the state matrix the same. The second row is shifted over one column to the left, wrapping around. The third row is shifted two columns, the fourth row by three. Wikipedia puts it nicely: "the importance of this step is to avoid the columns being encrypted independently, in which case AES degenerates into four independent block ciphers."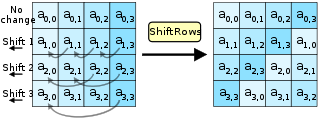



The diagram (and the AES specification) show the ShiftRows operation occuring in column-major notation. However, the sample code below uses row-major notation for the state matrix as it is more natural in Python. As long as the same notation is used each time the matrix is accessed, the final result is identical. Due to access patterns and cache behaviour, using one type of notation can lead to better performance.

MixColumns is more complex. It performs Matrix multiplication in Rijndael's Galois field between the columns of the state matrix and a preset matrix. Each single byte of each column therefore affects all the bytes of the resulting column. The implementation details are nuanced; this page and Wikipedia do a good job of covering them.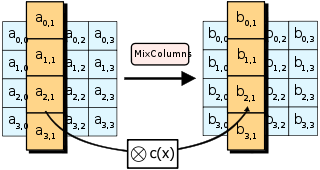



We've provided code to perform MixColumns and the forward ShiftRows operation. After implementing inv_shift_rows, take the state, run inv_mix_columns on it, then inv_shift_rows, convert to bytes and you will have your flag.

Challenge files:
  - diffusion.py

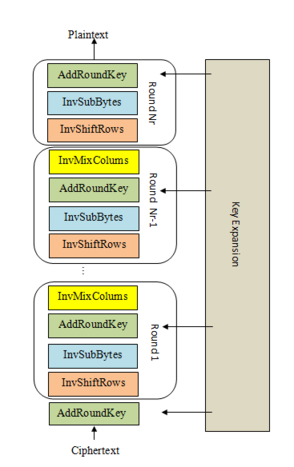
Apart from the KeyExpansion phase, we've sketched out all the components of AES. We've shown how SubBytes provides confusion and ShiftRows and MixColumns provide diffusion, and how these two properties work together to repeatedly circulate non-linear transformations over the state. Finally, AddRoundKey seeds the key into this substitution-permutation network, making the cipher a keyed permutation.

Decryption involves performing the steps described in the "Structure of AES" challenge in reverse, applying the inverse operations. Note that the KeyExpansion still needs to be run first, and the round keys will be used in reverse order. AddRoundKey and its inverse are identical as XOR has the self-inverse property.

We've provided the key expansion code, and ciphertext that's been properly encrypted by AES-128. Copy in all the building blocks you've coded so far, and complete the decrypt function that implements the steps shown in the diagram. The decrypted plaintext is the flag.

Yes, you can cheat on this challenge, but where's the fun in that?

The code used in these exercises has been taken from Bo Zhu's super simple Python AES implementation, so we've reproduced the license here.

Challenge files:
  - aes_decrypt.py
  - LICENSE

Resources:
  - Rolling your own crypto: Everything you need to build AES from scratch

The previous set of challenges showed how AES performs a keyed permutation on a block of data. In practice, we need to encrypt messages much longer than a single block. A mode of operation describes how to use a cipher like AES on longer messages.

All modes have serious weaknesses when used incorrectly. The challenges in this category take you to a different section of the website where you can interact with APIs and exploit those weaknesses. Get yourself acquainted with the interface and use it to take your next flag!

Play at https://aes.cryptohack.org/block_cipher_starter

It is essential that keys in symmetric-key algorithms are random bytes, instead of passwords or other predictable data. The random bytes should be generated using a cryptographically-secure pseudorandom number generator (CSPRNG). If the keys are predictable in any way, then the security level of the cipher is reduced and it may be possible for an attacker who gets access to the ciphertext to decrypt it.

Just because a key looks like it is formed of random bytes, does not mean that it necessarily is. In this case the key has been derived from a simple password using a hashing function, which makes the ciphertext crackable.

For this challenge you may script your HTTP requests to the endpoints, or alternatively attack the ciphertext offline. Good luck!

Play at https://aes.cryptohack.org/passwords_as_keys

Here you can encrypt in CBC but only decrypt in ECB. That shouldn't be a weakness because they're different modes... right?

Play at https://aes.cryptohack.org/ecbcbcwtf

ECB is the most simple mode, with each plaintext block encrypted entirely independently. In this case, your input is prepended to the secret flag and encrypted and that's it. We don't even provide a decrypt function. Perhaps you don't need a padding oracle when you have an "ECB oracle"?

Play at https://aes.cryptohack.org/ecb_oracle

You can get a cookie for my website, but it won't help you read the flag... I think.

Play at https://aes.cryptohack.org/flipping_cookie

I'm just a lazy dev and want my CBC encryption to work. What's all this talk about initialisations vectors? Doesn't sound important.

Play at https://aes.cryptohack.org/lazy_cbc

Data Encryption Standard was the forerunner to AES, and is still widely used in some slow-moving areas like the Payment Card Industry. This challenge demonstrates a strange weakness of DES which a secure block cipher should not have.

Play at https://aes.cryptohack.org/triple_des

Challenge contributed by randomdude999

Some block cipher modes, such as OFB, CTR, or CFB, turn a block cipher into a stream cipher. The idea behind stream ciphers is to produce a pseudorandom keystream which is then XORed with the plaintext. One advantage of stream ciphers is that they can work of plaintext of arbitrary length, with no padding required.

OFB is an obscure cipher mode, with no real benefits these days over using CTR. This challenge introduces an unusual property of OFB.

Play at https://aes.cryptohack.org/symmetry

I've struggled to get PyCrypto's counter mode doing what I want, so I've turned ECB mode into CTR myself. My counter can go both upwards and downwards to throw off cryptanalysts! There's no chance they'll be able to read my picture.

Play at https://aes.cryptohack.org/bean_counter

There may be a lot of redundancy in our plaintext, so why not compress it first?

Play at https://aes.cryptohack.org/ctrime

Before using the network, you must authenticate to Active Directory using our timeworn CFB-8 logon protocol.

Connect at socket.cryptohack.org 13399

Challenge files:
  - 13399.py


Challenge contributed by $in

Talk to me and hear a sentence from my encrypted stream of consciousness.

Play at https://aes.cryptohack.org/stream_consciousness

I don't trust other developers so I made my own ChaCha20 implementation. In this way, I am sure you will never be able to read my flag!

Challenge files:
  - chacha20.py
  - output.txt


Challenge contributed by yaumn and Synacktiv

Here's the start of my fast network authentication protocol, so far I've only implemented the "Ping" command so there shouldn't be any way to recover the key.

Play at https://aes.cryptohack.org/oh_snap

Challenge contributed by randomdude999

Sometimes the classic challenges can be the most delicious

Connect at socket.cryptohack.org 13421

Challenge files:
  - 13421.py


Challenge contributed by Eli Sohl

The first twist of the classic challenge, how can you handle an oracle with errors?

Connect at socket.cryptohack.org 13422

Challenge files:
  - 13422.py


Challenge contributed by Eli Sohl

This oracle lies! Can you still recover the message XOR are you going to have to give up?

Connect at socket.cryptohack.org 13423

Challenge files:
  - 13423.py


Challenge contributed by Eli Sohl

I've found an authenticated encryption mode called Infinite Garble Extension where an error in a single bit will corrupt the rest of the ciphertext. Seems like a great way to protect chat messages from attacks using bitflipping, padding oracles etc?

Play at https://aes.cryptohack.org/paper_plane

Challenge contributed by VincBreaker

Galois Counter Mode (GCM) is the most widely used block cipher mode in TLS today. It's an "authenticated encryption with associated data" cipher mode (AEAD), yet not resistant to misuse.

See here for a great resource on the inner workings of GCM, as well as this attack.

Play at https://aes.cryptohack.org/forbidden_fruit

Welcome to my military grade encryption service! It's based on AES but with some tweaks to make it NSA-proof.

Connect at socket.cryptohack.org 13406

Challenge files:
  - 13406.py


Challenge contributed by yaumn and Synacktiv