Hash Functions
A hash function is a function which takes an arbitrary long string of bits and produces a fixed-length output. Hash functions have applications in data structures, string-searching and even in video game design. Here we're interested in a subset of hash functions which are suitable for cryptographic purposes.
Cryptographic hash functions are designed to be one-way: functions that are practically impossible to invert. This is in contrast to the functions used in asymmetric cryptography, where trapdoor functions are infeasible to invert unless some additional secret knowledge is known.
Cryptographic hash functions are used to verify message integrity, compute digital signatures, and safely store passwords in databases. In asymmetric cryptography, hash functions are particularly useful in compressing arbitrary length messages to a value which has a smaller bit-length than the modulus when signing messages with RSA or protocols such as (EC)DSA or Elgamal.
For a hash function to be cryptographically secure, it must be resistant to the following three attacks:
- Pre-image attacks: given the output of a hash function
x = hash(m), it must be practically impossible to find a messagem0such thathash(m0) = x. This is another way of saying that the hash must be a one-way function. - Second pre-image resistance: given a message
m1, it must be practically impossible to find a messagem2such thathash(m1) = hash(m2). - Collision resistance: it should be practically impossible to find two messages
m1, m2such thathash(m1) = hash(m2). Note the difference to the second pre-image attack, in that we can vary bothm1andm2.
We can think of this as a linked set of dependencies, if a pre-image attack is known, so are second pre-image attacks and collision attacks. But if a collision attack is known, this doesn't generically allow pre-image attacks against the hash function.
Ultimately, it is impossible for a hash function to be totally secure against these attacks, in the same way symmetric and asymmetric ciphers can have their protocols brute forced. Even given a perfect one-way function, as the output has a fixed length, there will be infinitely many inputs that yield any chosen output. The goal for a cryptographic hash function is then to have algorithms designed to make the above problems "sufficiently" hard assuming an attackers compute power.
In the following challenges, we present custom hash functions which do not meet these criteria, or older cryptographic hash functions which have been found to be vulnerable to attacks.

Probability
Toggle-
Jack's Birthday Hash20 pts · 3300 Solves · 13 SolutionsToday is Jack's birthday, so he has designed his own cryptographic hash as a way to celebrate.
Reading up on the key components of hash functions, he's a little worried about the security of theJACK11hash.
Given any input data,JACK11has been designed to produce a deterministic bit array of length 11, which is sensitive to small changes using the avalanche effect.
UsingJACK11, his secret has the hash value:JACK(secret) = 01011001101.
Given no other data of theJACK11hash algorithm, how many unique secrets would you expect to hash to have (on average) a 50% chance of a collision with Jack's secret?You must be logged in to submit your flag.
Jack's Birthday Confusion30 pts · 2839 Solves · 11 SolutionsThe last computation has made Jack a little worried about the safety of his hash, and after doing some more research it seems there's a bigger problem.
Given no other data of theJACK11hash algorithm, how many unique secrets would you expect to hash to have (on average) a 75% chance of a collision between two distinct secrets?
Remember, given any input data,JACK11has been designed to produce a deterministic bit array of length 11, which is sensitive to small changes using the avalanche effect.You must be logged in to submit your flag.
Collisions
Toggle-
Collider50 pts · 2277 Solves · 8 SolutionsCheck out my document system about particle physics, where every document is uniquely referenced by hash.
Connect atsocket.cryptohack.org 13389
Challenge files:
- 13389.py
You must be logged in to submit your flag.
Hash Stuffing50 pts · 1408 Solves · 12 SolutionsWith all the attacks on MD5 and SHA1 floating around, we thought it was time to start rolling our own hash algorithm. We've set the block size to 256 bits, so I doubt anyone will find a collision.
Connect atsocket.cryptohack.org 13405
Challenge files:
- source.py
You must be logged in to submit your flag.
PriMeD5100 pts · 1024 Solves · 10 SolutionsPrimality checking is expensive so I made a service that signs primes, allowing anyone to quickly check if a number is prime.
The solution requires ~5 minutes to calculate on a commodity PC.
Connect atsocket.cryptohack.org 13392
Challenge files:
- 13392.py
Challenge contributed by randomdude999You must be logged in to submit your flag.
Twin Keys100 pts · 655 Solves · 5 SolutionsCryptohack's secure safe requires two keys to unlock its secret. However, Jack and Hyperreality can't remember the keys, only the start of one of them. Can you help find the lost keys to unlock the safe?
Connect atsocket.cryptohack.org 13397
Challenge files:
- 13397.py
Challenge contributed by ciphrYou must be logged in to submit your flag.
No Difference175 pts · 678 Solves · 16 SolutionsIt's easy to come across a collision for MD5, but can you find one in my custom hash function?
Connect atsocket.cryptohack.org 13395
Challenge files:
- 13395.py
Challenge contributed by VincBreakerYou must be logged in to submit your flag.
Length Extension
Toggle-
MD080 pts · 1245 Solves · 12 SolutionsI've invented a nice simple version of HMAC authentication, hopefully it isn't vulnerable to the same problems as Merkle–Damgård construction hash functions...
Connect atsocket.cryptohack.org 13388
Challenge files:
- 13388.py
Challenge contributed by randomdude999You must be logged in to submit your flag.
MDFlag125 pts · 423 Solves · 7 SolutionsMD0 had a serious weakness, here is a new improved MD5-based HMAC.
Connect atsocket.cryptohack.org 13407
Challenge files:
- 13407.py
Challenge contributed by giladkYou must be logged in to submit your flag.
Pre-image attacks
Toggle-
Mixed Up120 pts · 691 Solves · 6 SolutionsDue to the properties of XOR and hash functions, it shouldn't be possible to unmix the flag... or is it?
Connect atsocket.cryptohack.org 13402
Challenge files:
- 13402.py
Challenge contributed by giladkYou must be logged in to submit your flag.
Invariant250 pts · 347 Solves · 5 SolutionsIt's said that you shouldn't roll your own hash function. But how easy is it to break one?
Connect atsocket.cryptohack.org 13393
Challenge files:
- 13393.py
Challenge contributed by CryptanalyseYou must be logged in to submit your flag.
Hash-based Cryptography
Toggle-
Merkle Trees25 pts · 424 Solves · 8 SolutionsA Merkle tree is a fundamental concept in computer science, particularly utilized within blockchain technology and cryptocurrencies to ensure data integrity and efficiency in verification processes. Imagine it as a tree structure, but instead of leaves and branches in the traditional sense, it consists of nodes containing hashes of data blocks.
At the very bottom of the tree, are the leaves, which are hashes of individual pieces of data (like transactions in the case of cryptocurrencies). These hashes are unique fingerprints of the data, created using cryptographic hash functions that turn any input into a fixed-size, indecipherable output. Moving up the tree, each leaf node is paired and hashed together to form the nodes of the next layer. This pairing and hashing continue upwards until you reach the single hash at the top of the tree, known as the Merkle root.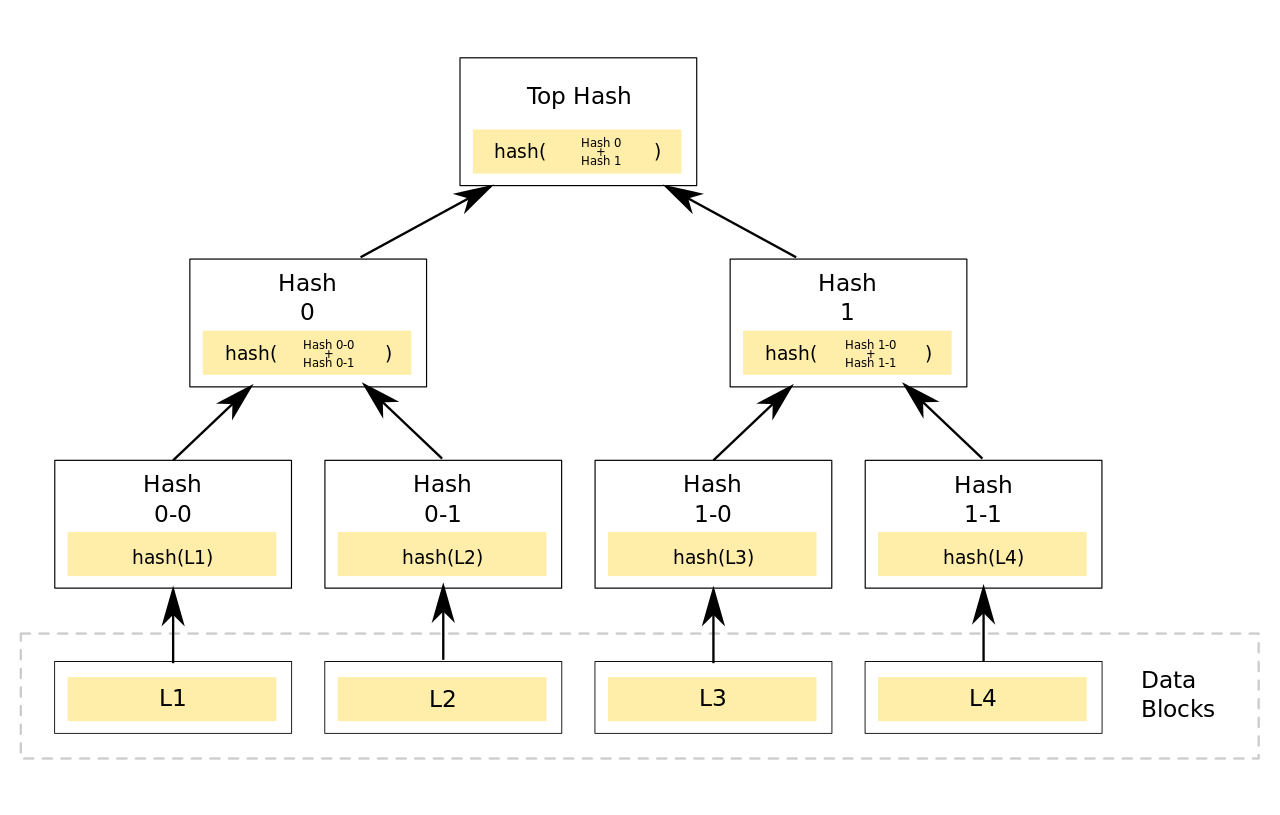
The beauty of the Merkle tree lies in its efficiency for verifying content. If you want to check if a specific piece of data is included in the set, you don't need to review the entire dataset. Instead, you only need to look at the hashes along the path from the specific item to the Merkle root. This significantly reduces the amount of data to be processed and verified, making Merkle trees useful for large datasets.
For this warmup challenge, you will be given a number of Merkle trees, each with four leaf nodes representing the hashes of the 4 data blocks, and each with a root node hash.
The SHA256 hash function will be used, and nodes will be paired by hashing the result of adding them together.
Each line inoutput.txtwill represent a bit of the flag depending on whether the Merkle tree proof correctly verifies or not.
(1 if the proof is validated, 0 otherwise)
Concatenate all these bits and convert to ASCII to get the flag.
Challenge files:
- generate.py
- output.txt
Challenge contributed by EctarioYou must be logged in to submit your flag.
WOTS Up75 pts · 346 Solves · 4 SolutionsWith the need to find post-quantum schemes, hash-based signatures are cool again. Challenge originally featured in ECSC 2023 (Norway).
Challenge files:
- chal.py
- data.json
You must be logged in to submit your flag.
WOTS Up 290 pts · 322 Solves · 5 SolutionsLevel Up

You are now level Current level