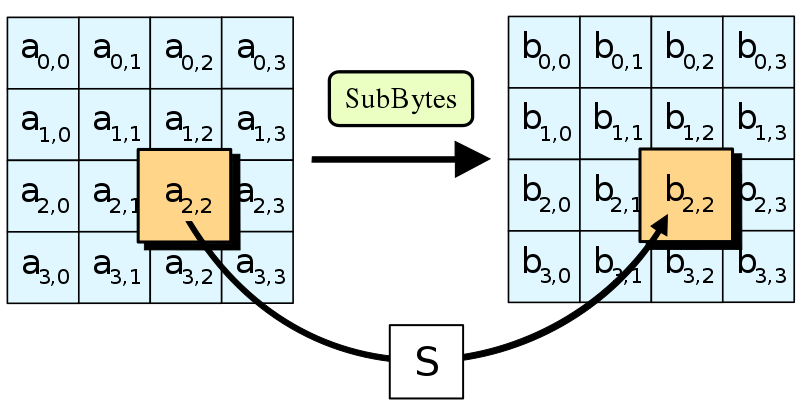
The first step of each AES round is SubBytes. This involves taking each byte of the state matrix and substituting it for a different byte in a preset 16x16 lookup table. The lookup table is called a "Substitution box" or "S-box" for short, and can be perplexing at first sight. Let's break it down.



In 1945 American mathematician Claude Shannon published a groundbreaking paper on Information Theory. It identified "confusion" as an essential property of a secure cipher. "Confusion" means that the relationship between the ciphertext and the key should be as complex as possible. Given just a ciphertext, there should be no way to learn anything about the key.

If a cipher has poor confusion, it is possible to express a relationship between ciphertext, key, and plaintext as a linear function. For instance, in a Caesar cipher, ciphertext = plaintext + key. That's an obvious relation, which is easy to reverse. More complicated linear transformations can be solved using techniques like Gaussian elimination. Even low-degree polynomials, e.g. an equation like x^4 + 51x^3 + x, can be solved efficiently using algebraic methods. However, the higher the degree of a polynomial, generally the harder it becomes to solve – it can only be approximated by a larger and larger amount of linear functions.

The main purpose of the S-box is to transform the input in a way that is resistant to being approximated by linear functions. S-boxes are aiming for high non-linearity, and while AES's one is not perfect, it's pretty close. The fast lookup in an S-box is a shortcut for performing a very nonlinear function on the input bytes. This function involves taking the modular inverse in the Galois field 2**8 and then applying an affine transformation which has been tweaked for maximum confusion. The simplest way to express the function is through the following high-degree polynomial: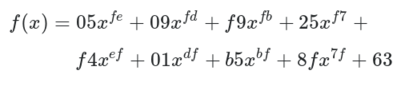



To make the S-box, the function has been calculated on all input values from 0x00 to 0xff and the outputs put in the lookup table.

Implement sub_bytes, send the state matrix through the inverse S-box and then convert it to bytes to get the flag.

Challenge files:
  - sbox.py

You have solved this challenge! View solutions

You must be logged in to submit your flag.